——并行符号枚举发现物理规律
 打印
打印
在国家自然科学基金项目(批准号:92270118、62276269)等资助下,中国人民大学孙浩教授团队提出了一种数据驱动科学发现的高效计算新范式。该团队发展的并行符号枚举方法(Parallel Symbolic Enumeration, PSE),能够从有限观测数据中高效、准确地发现物理规律的数学表达式。研究成果以“Discovering physical laws with parallel symbolic enumeration”为题,2025年11月21日在线发表于国际学术期刊《自然-计算科学》(Nature Computational Science)杂志上,论文链接:https://doi.org/10.1038/s43588-025-00904-8。
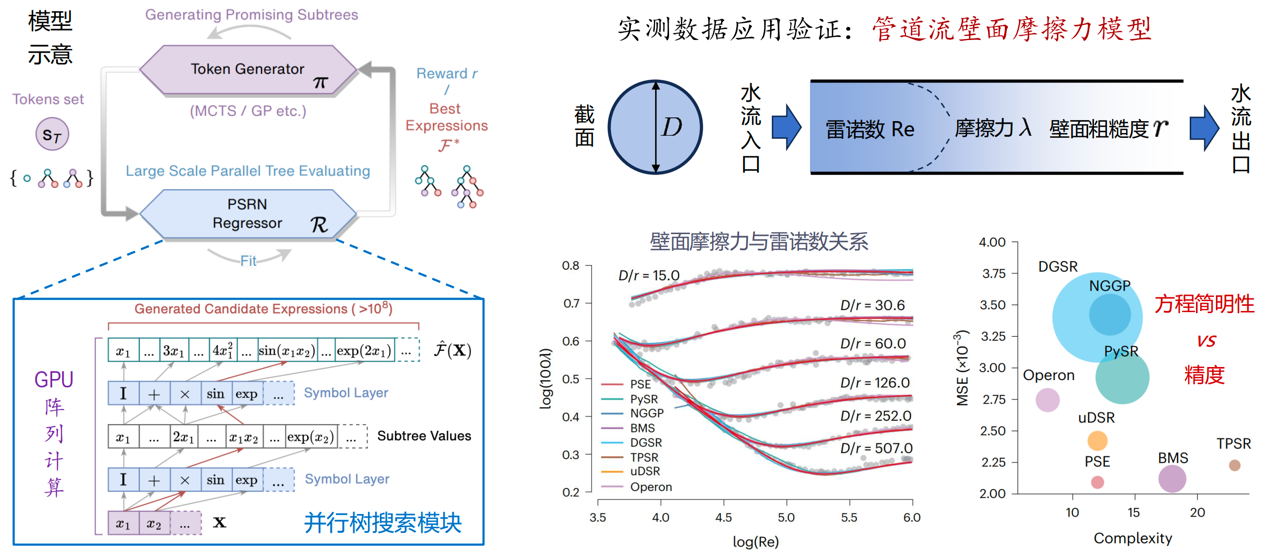
图 并行符号枚举方法及应用案例
从数据中自动发现简洁、可解释的数学表达式(即符号回归),在天文、材料、物理和生物等领域具有广泛的应用前景。然而,符号回归的核心挑战在于其巨大的搜索空间,潜在表达式的数量会随着复杂度的增加而组合爆炸,这是一个NP难问题。现有的算法(如遗传规划、深度学习等),在处理复杂问题时面临着准确性和效率的瓶颈,通常独立评估每一个候选表达式,导致大量的重复计算,不仅效率低下,而且难以发现复杂、高维问题背后的真实规律,成为制约该领域发展的挑战性难题。
为此,研究团队提出了并行符号枚举方法(PSE),旨在突破符号回归的效率与准确性瓶颈。该方法的核心是并行符号回归网络(PSRN),与传统方法不同,PSRN能够自动识别并复用不同数学表达式中的公共子树,从根本上避免了冗余计算。同时,该网络充分利用GPU的并行计算能力,可在数秒内同时评估数亿个候选表达式,实现了搜索效率的指数级提升。通过与指令生成器(如遗传编程)的迭代结合,PSE能够逐步构建并发现更复杂的公式。
研究团队在超过200个涵盖合成基准和真实物理实验(如混沌动力系统、机电定位系统、湍流摩擦定律)的符号回归问题集上系统验证了PSE的性能。实验结果表明,与当前国际主流算法相比,PSE在符号恢复准确率上最高可提升99%,同时计算速度快一个数量级以上,展现了较强的准确性、效率和可扩展性。该工作为数据驱动科学发现提供了一个高效、可扩展的计算框架,为自动化探索物理规律开辟了新路径,有望加速物理、材料、天文和生物等多个交叉学科领域的科学探索进程。
