 打印
打印
在国家自然科学基金项目(批准号:12125206、12588201、W2411003)资助下,中国科学院力学研究所蒋敏强研究员与合作者在非德拜声子理论研究方面取得进展。研究成果以“固体声子统一理论与非德拜反常相图(Unified theory of phononsin solids with phase diagram of non-Debye anomalies)”为题,于2025年10月7日发表于《自然·物理学》(Nature Physics)上,论文链接:https://www.nature.com/articles/s41567-025-03057-7。
固体宏观变形根据是否能恢复到初始状态可分为弹性和塑性两种模式。其中,弹性是固体内部晶格振动的连续介质极限,而塑性本质上是晶格发生不可逆重排的动力学过程。研究表明,晶格振动的反常在时空上往往预示着晶格发生塑性重排。因此,如何精确刻画晶格的反常振动,为理解含缺陷晶体、拓扑或化学无序固体等复杂体系的塑性变形机制提供了全新视角。1912年德拜在连续介质弹性波假设基础之上建立了晶格振动的声子理论,该经典理论无法描述已发现的两类晶格反常振动现象:一是当振动波长趋于晶格常数时,晶格的长程周期性导致声子态密度出现一些数学上不可导奇点,即范霍夫奇点(Van Hove singularity, VHS);二是当晶格失去长程周期性时,低频声子偏离德拜预测出现态密度过剩而形成玻色峰(boson peak, BP)。关于玻色峰的物理起源及其与范霍夫奇点是否等效仍存在长期争议。
针对该问题,蒋敏强研究员与合作者从声子散射的物理规律入手,理论推导了多自由度晶格振动的阻尼系数,以及考虑阻尼软化的声子频率-波数色散关系,实现了从低波数瑞利散射到高波数米氏散射转变的光滑描述,将德拜线性色散拓展至非线性空间。在声子动力学格林响应函数框架下,得到了可统一描述有序晶体和无序固体(玻璃等)的声子态密度解析表达。研究团队在此基础上,以散射体特征尺寸和散射声子平均自由程为参数空间,构建了非德拜声子反常的全景相图。分析发现,如果声子色散呈现非线性连续软化,则玻色峰和范霍夫奇点可由同一实体演变为高度耦合且可相互转换的两个变体;如果声子强烈散射导致色散出现额外的局域共振软化,则玻色峰和范霍夫奇点可作为完全不同的现象而独立地同时涌现,两者共存的相边界可由散射条件精确确定。最后,研究团队还计算了非德拜声子反常引起的低温比热行为,并得到了涵盖有序晶体到无序玻璃的143个真实固体的实验数据证实(其中55个数据由本工作测量得到),这表明建立的声子统一理论具有广泛的普适性和有效性。
上述发现不仅澄清了玻色峰的物理起源及其与范霍夫奇点的关系,还加深了对真实固体连续介质弹性极限和塑性重排的基本理解。
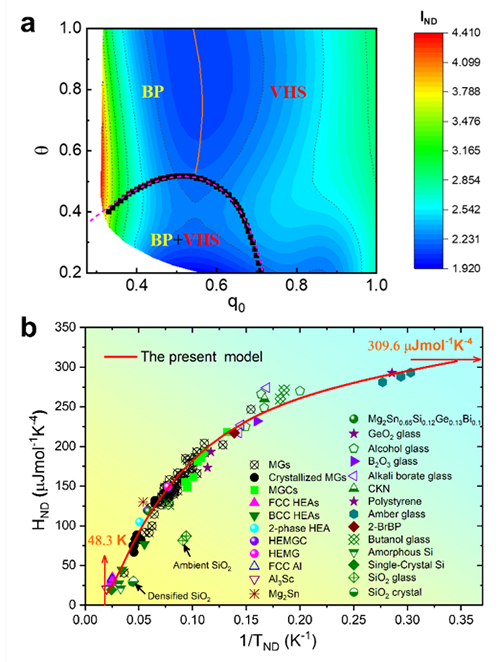
图 固体声子统一理论:(a)“玻色峰和范霍夫奇点”非德拜反常全景相图;(b)143种真实固体低温比热数据验证
